Wavegrad2

WaveGrad2: 文本到语音合成的迭代细化

摘要

本文介绍了 WaveGrad 2，一种用于文本到语音合成的非自回归生成模型。 WaveGrad 2 被训练来估计给定音素序列的波形的对数条件密度的梯度。该模型采用输入音素序列，并通过迭代细化过程生成音频波形。这与原始的 WaveGrad 声码器形成对比，后者以由单独模型生成的梅尔频谱图特征为条件。迭代细化过程从高斯噪声开始，通过一系列细化步骤（例如 50 步），逐步恢复音频序列。 WaveGrad 2 通过调整细化步骤的数量，提供了一种在推理速度和样本质量之间进行权衡的自然方式。实验表明，该模型可以生成高保真音频，接近最先进的神经 TTS 系统的性能。我们还报告了对不同模型配置的各种消融研究。

Introduction

深度学习彻底改变了文本到语音 (TTS) 合成。 文本到语音是一个多模态生成问题，它将输入文本序列映射到具有许多可能变化的语音序列，例如韵律、说话风格和发音模式。 大多数神经 TTS 系统遵循两阶段生成过程。 在第一步中，特征生成模型从文本或音素序列生成中间表示，通常是线性或梅尔谱图。 中间表示控制波形的结构，通常由自回归架构生成以捕获丰富的分布。 接下来，声码器将中间特征作为输入并预测波形。 因为它在推理过程中将来自特征生成模型的预测特征作为输入，所以声码器通常使用预测特征作为输入进行训练。

尽管这种两级 TTS 管道可以产生高保真音频，但部署可能很复杂，因为它使用了级联的学习模块。 另一个问题与通常主要根据经验选择的中间特征有关。 例如，mel-spectrogram 功能通常运行良好，但可能不是所有应用程序的最佳选择。 相比之下，数据驱动的端到端方法的好处已在机器学习的各种任务领域中得到广泛观察。 端到端方法能够从训练数据中自动学习最好的中间特征，这些特征通常是特定于任务的。 它们也更容易训练，因为它们不需要在不同阶段的监督和Ground-truth信号。

有两种主要的端到端 TTS 模型。自回归模型提供易于处理的似然计算，但它们需要在推理时反复生成波形样本，这可能很慢。相比之下，非自回归模型能够实现高效的并行生成，但它们需要令牌持续时间信息。用于训练的参考标记持续时间通常由离线强制对齐模型计算。为了预测生成的持续时间，训练了一个额外的模块来预测真实的持续时间。最近的工作侧重于将非自回归模型应用于端到端 TTS。然而，他们仍然依赖谱损失和梅尔谱图进行对齐，并且没有充分利用端到端的训练。 Fast Speech 2 需要额外的调节信号，例如音调和能量，以减少候选输出序列的数量。 EATS 使用对抗训练以及频谱图损失来处理一对多映射问题，这使得架构更加复杂。

在这项工作中，我们提出了 WaveGrad 2，这是一种非自回归音素到波形模型，不需要中间特征或专门的损失函数。为了使架构更加端到端，WaveGrad 解码器被集成到 Tacotron 2 式非自回归编码器中。 WaveGrad 解码器从随机噪声开始迭代优化输入信号，并且可以产生具有足够步长的高保真音频。一对多映射问题由分数匹配目标score matching objective处理，该目标优化对数似然的加权变分下界。

非自回归编码器遵循最近提出的非注意力 Tacotron，它结合了文本编码器和高斯重采样层以合并持续时间信息。在训练期间使用Ground-truth持续时间信息，并训练持续时间预测器来估计它。在推理过程中，持续时间预测器预测每个输入标记的持续时间。与基于注意力的模型相比，这种持续时间预测器对注意力失败的弹性明显更强，并且由于计算位置的方式而保证了单调对齐。本文的主要贡献如下：

• 一种完全可微且高效的架构，可直接生成波形而无需显式生成频谱图等中间特征；
• 通过改变细化步骤的数量在保真度和生成速度之间提供自然权衡的模型；
• 端到端非自回归模型达到 4.43 平均意见得分 (MOS)，接近最先进的神经 TTS 系统的性能。

Score matching

与最初的 WaveGrad 类似，WaveGrad 2 建立在分数匹配 和扩散概率模型 (diffusion probabilistic models) 的先前工作之上。 在 TTS 的情况下，得分函数被定义为对数条件分布 \(p(y | x)\) 相对于输出 \(y\)​ 的梯度为 \[ \begin{equation}\label{eqa1} s(y | x) = ∇_y \text{ log } p(y | x), \end{equation} \] 其中 \(y\) 是波形，\(x\) 是conditioning signal。 为了在给定条件信号的情况下合成语音，可以通过Langevin dynamics从初始化 \(y ̃_0\) 开始迭代地绘制波形为 \[ \begin{equation}\label{eqa2} y ̃_{i + 1} = y ̃_i + \frac{η}{2} s ( y ̃_i | x ) + \sqrt η z_i, \end{equation} \] 其中 \(η > 0\) 是步长，\(z_i ∼ N(0,I)\)，\(I\) 表示单位矩阵。

继之前的工作之后，我们采用了一种特殊的参数化方法，称为扩散模型(diffusion model)。 评分网络 \(s(y ̃ | x, α ̄)\)​ 被训练通过最小化模型预测和真实值 \(\epsilon\)​ 之间的距离来预测缩放导数，如下所示 \[ \begin{equation}\label{eqa3} E_{α ̄,\epsilon} [|| \epsilon_{\theta}(y ̃, x, \sqrt α ̄ ) - \epsilon||_1] \end{equation} \] 其中 \(\epsilon ∼ N (0, I )\)​ 是通过应用"重新参数化技巧"引入的噪声项，\(α ̄\) 是噪声水平，\(y ̃\)​​ 是根据以下公式采样的 \[ \begin{equation}\label{eqa4} y ̃ = \sqrt α ̄ y_0 + \sqrt {1-α ̄} \epsilon \end{equation} \] 在训练过程中，\(α ̄\)'s是从区间\([α ̄_n, α ̄_{n+1}]\)​​中基于一个预定义的\(\beta\)​​​的线性计划采样的，公式如下： \[ \begin{equation}\label{eqa5} α ̄_n:=􏰅\prod_{s=1}^n(1−β_s). \end{equation} \] 在每次迭代中，更新后的波形按照以下随机过程进行估计： \[ \begin{equation}\label{eqa6} y_{n−1}=\frac{1}{\sqrt \alpha_n} ( y_n− \frac{\beta_n} {\sqrt {1-α ̄_n}} \epsilon_θ(y_n,x, \sqrt α ̄_n) +σ_nz. \end{equation} \]

WaveGrad 2

wavegrad2-fig1

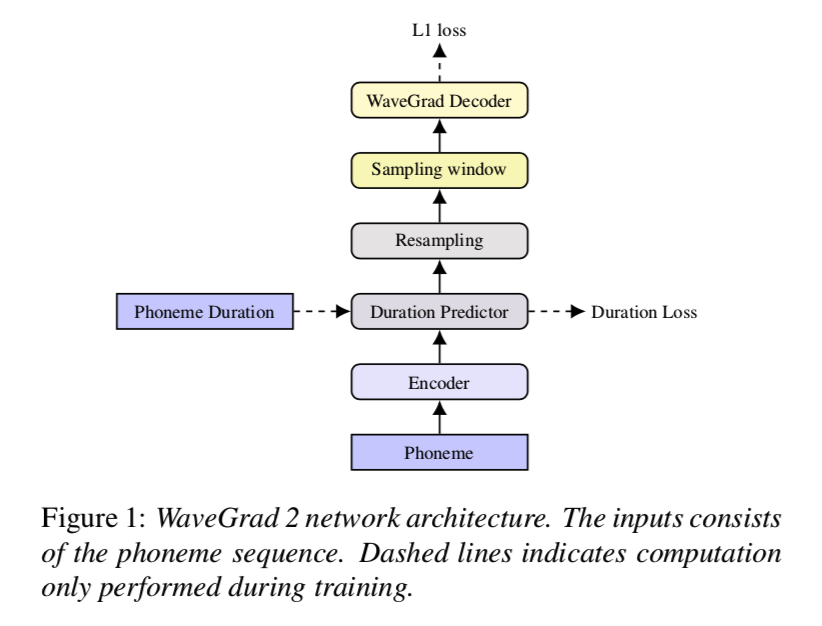
所提出的模型包括三个模块，如图1：

• 编码器将音素序列作为输入并从输入上下文中提取抽象的隐藏表示。
• 重采样层改变编码器输出的分辨率以匹配输出波形时间尺度，量化为 10ms 段（类似于典型的梅尔频谱图特征）。 这是通过在训练期间调节目标持续时间来实现的。 在推理期间利用持续时间预测器模块预测的持续时间。
• WaveGrad 解码器通过迭代改进有噪声的波形来预测原始波形。 在每次迭代中，解码器逐渐细化信号并添加细粒度的细节。

3.1 Encoder

编码器的设计遵循 Tacotron 2 的设计。 音素标记用作输入，在单词边界插入静音标记。 在每个句子之后添加一个序列结束标记。 标记首先转换为学习嵌入learned embedding，然后通过 3 个含dropout 的卷积层和批量归一化层。 最后，通过将输出传递到具有 ZoneOut 正则化的单个双向长短期记忆 (LSTM) 层，对长期上下文信息进行建模。

3.2 重采样

输出波形序列的长度与编码器表示的长度非常不同。 在 Tacotron 2 中，这是通过注意力机制解决的。 为了使结构非自回归和加速推理，我们采用了非注意力 Tacotron 中引入的高斯上采样。 高斯上采样不是根据其持续时间重复每个标记，而是同时预测持续时间和影响范围。 这些参数用于注意力权重计算，它完全依赖于预测的位置。 在训练期间，改为使用Ground-truth持续时间，并测量额外的均方损失以训练持续时间预测器。 这在图 1 中被标记为 Duration Loss。推理期间不需要真实持续时间，而是采用预测持续时间。

3.3 采样窗口

由于波形分辨率非常高（在我们的例子中为每秒 24,000 个样本），由于高计算成本和内存限制，计算一次话语中所有波形样本的损失是不可行的。 相反，在学习了整个输入序列的表示之后，我们对一个小片段进行采样以合成波形。 由于重采样层，编码器表示和波形样本已经对齐。 在每个小批量中单独采样随机段，并根据上采样率（在我们的设置中为 300）提取相应的波形段。 在推理期间使用完整的编码器序列（重采样后），这会在训练和推理之间引入小的不匹配。 我们进行消融研究以研究采样窗口大小如何影响第 4.1 节中的保真度。

3.4 解码器

wavegrad2-fig2

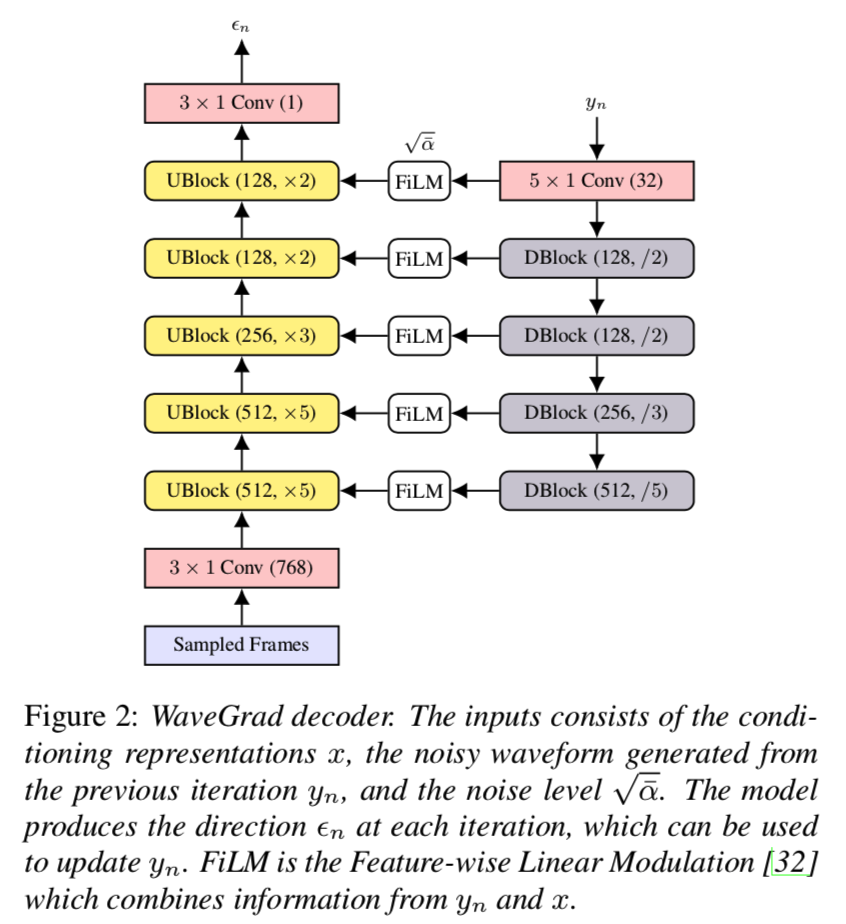
解码器逐渐对隐藏的表示进行上采样以匹配波形分辨率。 在我们的例子中，波形以 24 kHz 采样，我们需要上采样 300 倍。 这是使用 WaveGrad 解码器实现的，如图 2 所示。该架构包括 5 个上采样块 (UBlock) 和 4 个下采样块 (DBlock)。 在生成过程的每次迭代中，网络通过预测包含的噪声项 \(\epsilon_n\) 来对噪声输入波形估计 \(y_n\) 去噪，条件是隐藏表示遵循等式 6。如第 2 节所述，生成过程从 随机噪声估计 \(y_N\) ，并在 \(N\)​（通常设置为 1000)步上迭代细化它以生成波形样本。 在我们之前的工作之后，训练目标是预测和真实噪声项之间的 L1 损失。 在训练期间，使用单个随机采样迭代计算此损失。

结论

在本文中，我们提出了 WaveGrad 2，这是一种端到端的非自回归 TTS 模型，它以音素序列作为输入并直接合成波形，而不像大多数 TTS 系统那样使用手工设计的中间特征（例如，频谱图）。 与先前的工作类似，输出波形是通过从随机噪声开始的迭代细化过程生成的。 生成过程通过改变细化步骤的数量来提供保真度和速度之间的权衡。 实验表明，WaveGrad 2 能够生成与强基线相当的高保真音频。 探索不同模型配置的消融研究发现，增加模型大小是决定 WaveGrad 2 综合质量的最重要因素。 未来的工作包括在有限的细化迭代次数下提高性能。